Previous   Next
Parsing_04_tokenization Parsing_05_parsing_grammars_and_asts Parsing_06_evaluation

Parsing: (05) Parsing, Grammars and ASTs

Context Free Grammars, EBNF, and Abstract Syntax Trees

More on Parsing:

https://ucsb-cs56-pconrad.github.io/tutorials/parsing_05_parsing_grammars_and_asts

Acknowledgments: this series or articles is joint work, a collaboration between Kyle Dewey and Phill Conrad.

Parsing

Parsing involves recognizing structures that are made up of tokens. These structures can be large, and they may even be recursively defined (as with if-else statements). Such structures are usually referred to as Abstract Syntax Trees (ASTs). A breakdown of this term follows:

To better understand what an AST is, consider the following example. This shows an AST which resulted from parsing the tokens 1, +, 2:

1+2

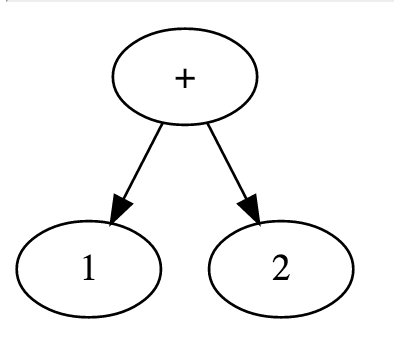
As shown, + forms the root of the tree, and it has the child nodes 1 and 2. Each of these is a leaf, which makes sense considering that integer constants simply evaluate to themselves without any other bits of code getting involved.

A more complex example is shown below, which uses the tokens from our running example. The actual tokens have been repeated below for convenience.

         
if ( x > 7
) { foo = 10
; } else { System
. err . println (
"FIX THIS CODE" ) ; }  

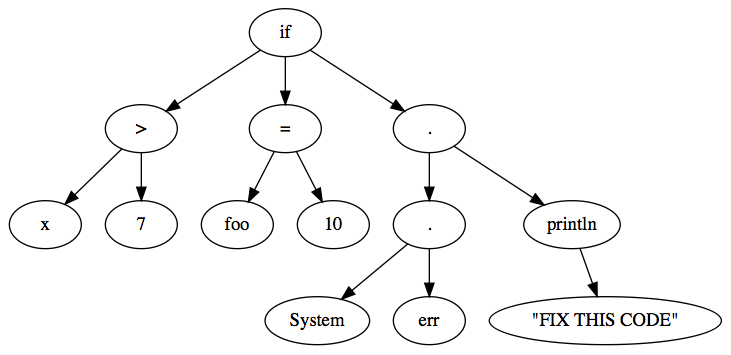
parsing_example

As shown in the above example, parsing takes operator precedence into account. Specifically, the parser knew to parse System.err.println(...) effectively as (System.err).println(...), as opposed ot the invalid System.(err.println(...)).

Parsing: turn sequence of tokens into an AST

In parsing, we turn a sequence of tokens into an Abstract Syntax Tree (AST).

For example, 2+3*5 starts as sequence of five characters. Or, if there is whitespace, perhaps 9 characters: 2 + 3 * 5

We then turn it into a sequence of tokens:

This is still not parsing.

A parser typically has two jobs.

Here’s an AST for 2+3*5. Note how the tree reflects the operator precedence.

Now lets dive into how a parser works with a grammar to check syntax and produce an AST.

Parsing: Grammars

Grammars are expressions of the rules of a language. A particular kind of grammar is called a “context-free grammar (CFG), and that’s the kind we are going to need to do parsing.

We won’t give a formal definition of what a CFG is since that’s a topic for CMPSC138. Instead, we’ll provide a “good enough” definition for what we’ll be doing with CFGs in this course. We’ll mostly do that by just giving examples, and explaining how to use those examples, rather than dwelling too much in the theory. You’ll get plenty of the theory in CMPSC138, CMPSC160 and CMPSC162.

One way of expressing a CFG is with a notation called Extended Backus-Naur Form (EBNF). Here’s the EBNF for a grammar for simple arithmetic expressions with +,-,*,/, integers, unary minus, and parentheses:

expression ::= additive-expression
additive-expression ::= multiplicative-expression ( ( '+' | '-' ) multiplicative-expression ) *
multiplicative-expression ::= primary ( ( '*' | '/' ) primary ) *
primary ::= '(' expression ')' | INTEGER | '-' primary

If this is your first time seeing a context-free grammar for a language, this may look bewildering and confusing. If so, be patient—there is more explanation below.

Before we go into that though, here is one more example. This example shows how the grammar above is modified to add six relational operators, == , != , < , <= , > , >=, and the exponentiation operator: ** into the language:

expression ::= comparison-expression
comparison-op ::= '==' | '!=' | '<' | '<=' | '>' | '>='
comparison-expression ::= additive-expression ( comparison-op additive-expression ) *
additive-expression ::= multiplicative-expression ( ( '+' | '-' ) multiplicative-expression ) *
multiplicative-expression ::= exponent-expression ( ( '*' | '/' ) exponent-expression ) *
exponent-expression ::= primary '**' exponent-expression | primary
primary ::= '(' expression ')' | INTEGER | '-' primary

Top Down Parsing

As you try to understand a grammar, there are two ways to think about it: top-down and bottom-up.

Our parser is a top-down parser, so we’ll start by explaning how top-down parsing works. Some students find it easier to understand top-down parsing if they first look at bottom up parsing. So if this explanation leaves your head spinning the first time you read it, just move on to the section below on “bottom-up” parsing, try to understand that, then re-read this section.

Suppose we want to parse 2+3*5.

To parse this top-down, we start with the first non-terminal in our grammar—that is, the left hand side of the first line of the grammar. That left hand side is the word expression. That is the start symbol of our grammar.

The start symbol is special because:

In the code, you’ll also see that the flow of control follows from the start symbol. In the starter code for F16 lab06, the parsing starts on this line of code, line 176 of Parser.java:

	final ParseResult<AST> rawResult = parseExpression(0);

The production for expression looks like this:

expression ::= additive-expression

And the code reflects this. If you look inside the code for parseExpression in Parser.java at line 144, you see that it calls a method called parseAdditiveExpression:

    private ParseResult<AST> parseExpression(final int pos) throws ParserException {
        return parseAdditiveExpression(pos);
    }

This process continues: you’ll see that every one of the parseXXXXX methods has a structure that corresponds to the production in the grammar. The things on the right hand side of a production are parsed by calls to parseXXXXX routines.

Turning back to the basic idea of parsing the expression 2+3*5.

We start out with expression and then we have to keep breaking it down by applying productions, until we have determined the correct way to represent 2+3*5 as an AST.

The tree we want is this one:

It turns out that the production in this case, the ones listed below, says that an additive-expression is either a multiplicative-expression, OR, its a multiplicative-expression followed by zero or more repetitions of + or - and another multiplicative-expression

additive-expression ::= multiplicative-expression ( ( '+' | '-' ) multiplicative-expression ) *

Some of our choices are:

We choose by looking at the sequence of tokens we have, and see which one is the best fit. In this case, the best fit is:

additive-expression ::= multiplicative-expression '+' multiplicative-expression

Bottom up parsing

Another way to parse, and/or to understand how a grammar is applied is to work bottom up.

Please note that the code in our parser does not work this way. I’m only going into this because some students find it easier to understnand how a grammar works if they see it “bottom-up” as well as top-down.

Note though, that the code in our parsing assignment is most definitely a top-down parser. Writing code for bottom-up parsers is considerably more challenging—you might do it in CMPSC160 or CMPSC162.

To parse 2+3*5 bottom up:

And the process continues in this manner, trying to put together something that eventually combines all of the input into something that reduces down to expression.

Tokenization

Tokenization involves converting larger sequences of characters into meaningful units (integers, operators, variables, keywords, etc.). Each of these units is called a “token”. To illustrate what tokens are, consider again the aforementioned Java code snippet, repeated below for convenience:

if (x > 7) { // magic number
  foo = 10;
} else {
  /* TODO: this needs a better solution
     right now this is broken */
  System.err.println( "FIX THIS CODE" );
}

This code snippet contains over 100 characters. However, it contains only 24 tokens, namely (put into a table to save space):

         
if ( x > 7
) { foo = 10
; } else { System
. err . println (
"FIX THIS CODE" ) ; }  

As shown, tokens separate semantically meaningful groupings of characters into individual units. For example, if, else, 10, "FIX THIS CODE", and others are considered individual, distinct tokens. Additionally, components extraneous to the code, such as unnecessary whitespace and comments, are completely stripped out. That said, there are still some “extra” components in here, such as the braces ({ and }). This is left for the next phase to handle, namely parsing.

Parsing

Parsing involves recognizing structures that are made up of tokens. These structures can be large, and they may even be recursively defined (as with if-else statements). Such structures are usually referred to as Abstract Syntax Trees (ASTs). A breakdown of this term follows:

To better understand what an AST is, consider the following example.

This shows an AST which resulted from parsing the string 1+2.

Then, the grammar is applied.

The recognition of the INTEGER terminal symbol in the grammar corresponds to the IntToken("1") object in our code. And from it, we construct an AST node for the 1. We end up doing the same thing for the 2, and then constructing an AST node for the + that has two children, the left and right operands of the + operation:

1+2

As shown, + forms the root of the tree, and it has the child nodes 1 and 2. Each of these is a leaf, which makes sense considering that integer constants simply evaluate to themselves without any other bits of code getting involved.

A more complex example is shown below, which uses the tokens from our running example. The actual tokens have been repeated below for convenience.

         
if ( x > 7
) { foo = 10
; } else { System
. err . println (
"FIX THIS CODE" ) ; }  

parsing_example

As shown in the above example, parsing takes operator precedence into account. Specifically, the parser knew to parse System.err.println(...) effectively as (System.err).println(...), as opposed ot the invalid System.(err.println(...)).

Evaluation (also called “interpretation)

Interpretation involves taking ASTs and recursively evaluating them to values. In a language like Java, this can get fairly complex, given the complexity of the overall language. As such, we will refrain from using the running example here. Instead, we’ll use a much simpler arithmetic expression language for the purpose of an example.

Consider the AST below, corresponding to the expression 3 * 4 + 2:

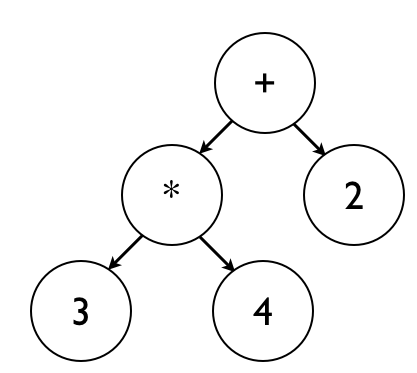
interp_01

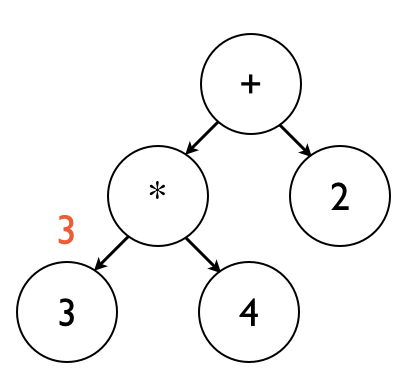
Evaluation starts at the top of the AST, which corresponds to the + node in this AST. The + node first finds the value of its left child, corresponding to the * node. Evaluation then proceeds to the * node, which gets the value of its left child. This leads evaluation to the 3 node. Because the constant 3 trivially evaluates to itself, evaluation returns 3 at this point. This is illustrated in the image below, which shows values returned from evaluation in red:

interp_02

Once the 3 node is complete, evaluation goes back to the * node, which gets the value of its right child. Evaluation then moves to the 4 node, which simply returns 4. This is illustrated below:

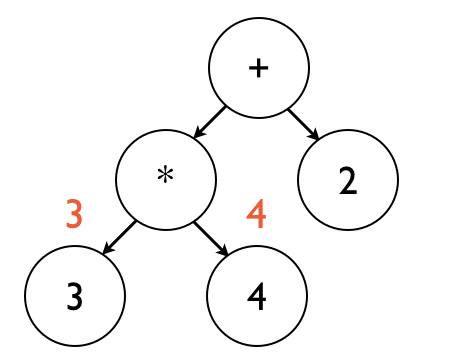
interp_03

Evaluation now proceeds to the * node, which finally has the values of both of its child nodes. From here, it multiplies these values together, and returns the result. This is illustrated below:

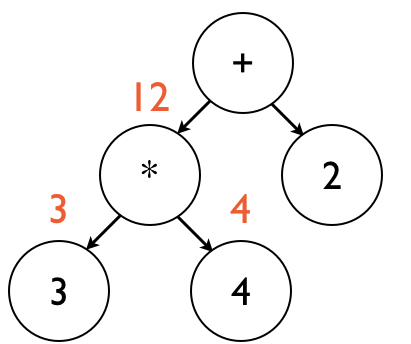
interp_04

At this point, evaluation returns to the + node, which now has the value of its left child (*). Evaluation then proceeds to the right child, which returns the constant 2, illustrated below:

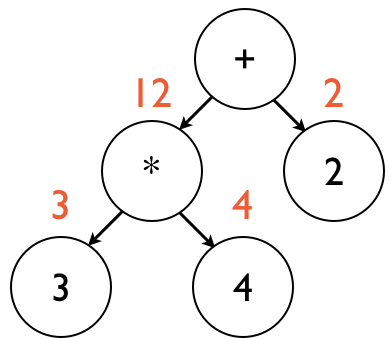
interp_05

The + node finally has the values of both of its children, and subsequently adds them together. This result is then returned. This is illustrated below:

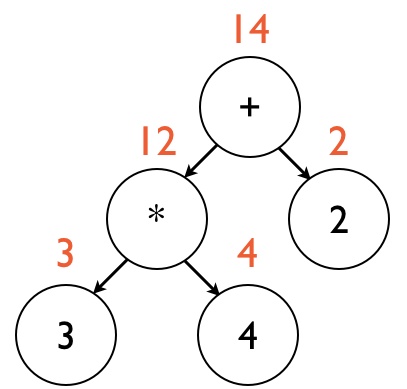
interp_06

Note that this entire process followed the general pattern of a recursive depth-first traversal.

Real world grammars

The two grammars above are relatively short and simple. A grammar for a full language such as Java or Python ends up being quite long and complex. However, you’ll see that the grammar has essentially a very similar structure. If you want to see some of those examples, here are links to them:

More on Parsing:

Previous   Next
Parsing_04_tokenization Parsing_05_parsing_grammars_and_asts Parsing_06_evaluation